Red-black trees in matchbox
I’m working on implementing red-black search trees in matchbox and have managed most of it by now. I still need to implement deletion and the re-balancing code for handling those, but I have insertion up and running. I have implemented both a set and a map type using red-black trees, but here I will only describe the set.
As is the idea with matchbox, the data structure is implemented using patterns-constructors, and for the set data type, I have defined the tree as this:
library(pmatch)
rbt_colours := RBT_BLACK | RBT_RED
rbt_set := RBT_SET_EMPTY |
RBT_SET(col : rbt_colours,
val,
left : rbt_set,
right : rbt_set)There is a third colour, “double black”, that I need when I get to deletion, but it isn’t needed for now. Trees are either empty or consist of a colour, a value, and two sub-trees.
I have a function for creating an empty tree:
empty_red_black_set <- function() RBT_SET_EMPTYand I can check if a tree is empty or if it contains a given value using these functions:
is_red_black_set_empty <- function(tree) {
t <- TRUE; f <- FALSE
pmatch::cases(
tree,
RBT_SET_EMPTY -> t,
otherwise -> f
)
}
rbt_set_member <- function(tree, v) {
t <- TRUE ; f <- FALSE
pmatch::cases(
tree,
RBT_SET_EMPTY -> f,
RBT_SET(col, val, left, right) -> {
if (val == v) t
else if (val > v) rbt_set_member(left, v)
else rbt_set_member(right, v)
}
)
}
rbt_set_member <- tailr::loop_transform(rbt_set_member)The reason I put TRUE and FALSE in local variables is simply that the lintr complains if I assign to the bool literals, but if I use variables the complaints go away. The membership function is tail-recursive, so I can translate it into a loop using tailr.
For inserting values, there is this re-balancing function:
rbt_set_balance <- function(tree) { # fixme: add deletion transformations
pmatch::cases(
tree,
RBT_SET(
RBT_BLACK,
z,
RBT_SET(RBT_RED,x,a,RBT_SET(RBT_RED,y,b,c)),
d
) -> RBT_SET(
RBT_RED,
y,
RBT_SET(RBT_BLACK,x,a,b),
RBT_SET(RBT_BLACK,z,c,d)
),
RBT_SET(RBT_BLACK,
z,
RBT_SET(RBT_RED,y,RBT_SET(RBT_RED,x,a,b),c),
d
) -> RBT_SET(
RBT_RED,
y,
RBT_SET(RBT_BLACK,x,a,b),
RBT_SET(RBT_BLACK,z,c,d)
),
RBT_SET(RBT_BLACK,
x,
a,
RBT_SET(RBT_RED,y,b,RBT_SET(RBT_RED,z,c,d))
) -> RBT_SET(
RBT_RED,
y,
RBT_SET(RBT_BLACK,x,a,b),
RBT_SET(RBT_BLACK,z,c,d)
),
RBT_SET(
RBT_BLACK,
x,
a,
RBT_SET(RBT_RED,z,RBT_SET(RBT_RED,y,b,c),d)
) -> RBT_SET(
RBT_RED,
y,
RBT_SET(RBT_BLACK,x,a,b),
RBT_SET(RBT_BLACK,z,c,d)
),
otherwise -> tree)
}It is invoked by the insertion function to re-establish the invariants of a red-black search tree. We call it every time we modify a tree in the insertion recursion, that looks like this:
rbt_set_insert_ <- function(tree, elm) {
if (is_red_black_set_empty(tree))
return(RBT_SET(RBT_RED, elm, RBT_SET_EMPTY, RBT_SET_EMPTY))
if (elm < tree$val)
rbt_set_balance(RBT_SET(
tree$col,
tree$val,
rbt_set_insert_(tree$left, elm),
tree$right)
)
else if (elm > tree$val)
rbt_set_balance(RBT_SET(
tree$col,
tree$val,
tree$left,
rbt_set_insert_(tree$right, elm))
)
else
tree # the value is already in the tree, at this level, so just return
}
rbt_set_insert <- function(tree, elm) {
tree <- rbt_set_insert_(tree, elm)
tree$col <- RBT_BLACK
tree
}There is two insertion functions because we need to set the root-colour to black, but only the root, so we have a special function that handles the root and another that handles the recursions.
That is it, now we have a red-black search tree.
tree <- empty_red_black_set()
for (v in 1:100)
tree <- rbt_set_insert(tree, v)
rbt_set_member(tree, 100)## [1] TRUE
rbt_set_member(tree, 101)## [1] FALSE
The insertion code is not tail-recursive, however. So we cannot use tailr to translate it into a looping function. We can make it tail-recursive, though, using a continuation to update the tree.
The rail-recursive function, in continuation-passing-style, looks like this:
make_left_cont <- function(tree, cont) {
force(tree) ; force(cont)
function(new_tree) {
cont(rbt_set_balance(
RBT_SET(
tree$col,
tree$val,
new_tree,
tree$right
)))
}
}
make_right_cont <- function(tree, cont) {
force(tree) ; force(cont)
function(new_tree) {
cont(rbt_set_balance(
RBT_SET(
tree$col,
tree$val,
tree$left,
new_tree
)))
}
}
rbt_set_insert_tr_ <- function(tree, elm, cont) {
if (is_red_black_set_empty(tree)) {
return(
cont(RBT_SET(RBT_RED,
elm,
RBT_SET_EMPTY,
RBT_SET_EMPTY)))
}
if (elm < tree$val) {
rbt_set_insert_tr_(
tree$left,
elm,
make_left_cont(tree, cont)
)
} else if (elm > tree$val) {
rbt_set_insert_tr_(
tree$right,
elm,
make_right_cont(tree, cont)
)
} else {
cont(tree)
}
}
rbt_set_insert_tr_ <- tailr::loop_transform(rbt_set_insert_tr_)
rbt_set_insert_tr <- function(tree, elm) {
tree <- rbt_set_insert_tr_(tree, elm, cont = identity)
tree$col <- RBT_BLACK
tree
}I have two functions for creating new continuations, one for inserting the result of the recursive call into a left-subtree and one for inserting the tree into a right-subtree. Normally, we would just use closures inside the rbt_set_insert_tr_ function, but this will not work after we have translated the function into a loop. There, references to tree will always be the most recent tree we are processing, but we need the continuations to remember the tree object at the time we create them. I achieve this by putting tree in the closure of these continuation-creating functions.
This function will work most of the time, but we are constructing continuations that potentially require very deep call-stacks. We can avoid this using the trampoline/thunk trick.1 Instead of calling continuations directly, we make thunks out of them. When we need to evaluate a continuation, we keep evaluating it as long as it returns thunks, and when it evaluates to a value, we are done. The trampoline/thunk function looks like this:
make_thunk <- function(f, ...) {
force(f)
params <- list(...)
function() do.call(f, params)
}
trampoline <- function(thunk) {
while (is.function(thunk)) thunk <- thunk()
thunk
}
make_left_cont <- function(tree, cont) {
force(tree) ; force(cont)
function(new_tree) {
make_thunk(
cont,
rbt_set_balance(RBT_SET(
tree$col,
tree$val,
new_tree,
tree$right
))
)
}
}
make_right_cont <- function(tree, cont) {
force(tree) ; force(cont)
function(new_tree) {
make_thunk(
cont,
rbt_set_balance(RBT_SET(
tree$col,
tree$val,
tree$left,
new_tree
))
)
}
}
rbt_set_insert_tr_ <- function(tree, elm, cont) {
if (is_red_black_set_empty(tree)) {
return(
trampoline(cont(RBT_SET(
RBT_RED,
elm,
RBT_SET_EMPTY,
RBT_SET_EMPTY
)))
)
}
if (elm < tree$val) {
rbt_set_insert_tr_(
tree$left,
elm,
make_left_cont(tree, cont)
)
} else if (elm > tree$val) {
rbt_set_insert_tr_(
tree$right,
elm,
make_right_cont(tree, cont)
)
} else {
trampoline(cont(tree))
}
}
rbt_set_insert_tr_ <- tailr::loop_transform(rbt_set_insert_tr_)
rbt_set_insert_tr <- function(tree, elm) {
tree <- rbt_set_insert_tr_(tree, elm, cont = identity)
tree$col <- RBT_BLACK
tree
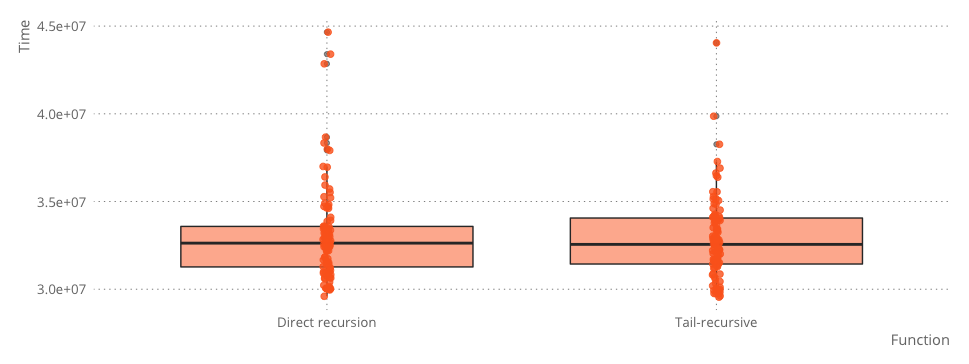
}We do not gain anything in running time with this exercise. The added complexity in the tail-recursive function makes the loop-version just as slow as the recursive function. We will not risk running out of call-stack with the tail-recursive function, however.
tree <- empty_red_black_set()
for (v in 1:100)
tree <- rbt_set_insert(tree, v)
library(microbenchmark)
bm <- microbenchmark(rbt_set_insert(tree, 120),
rbt_set_insert_tr(tree, 120))
bm## Unit: milliseconds
## expr min lq mean median uq
## rbt_set_insert(tree, 120) 30.71723 35.58180 42.49798 39.50093 45.44957
## rbt_set_insert_tr(tree, 120) 28.88509 35.53515 40.70564 38.54859 42.78433
## max neval
## 105.8753 100
## 107.9530 100
- You can read all about continuations and the trampoline/thunk trick in my book on Functional Programming in R. [return]